DETAILED SOLUTIONS AND CONCEPTS QUADRATIC EQUATIONS

PLEASE NOTE THAT YOU CANNOT USE A CALCULATOR ON THE ACCUPLACER - ELEMENTARY ALGEBRA TEST! YOU MUST BE ABLE TO DO THE FOLLOWING PROBLEMS WITHOUT A CALCULATOR!

Quadratic Equations

A quadratic equation in x is an equation that can be written in the standard form
, where a, b, and c are real numbers, but .

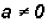Solving Quadratic Equations

A. Factoring Method - Some, but not all quadratic equations can be solved by factoring.

 •Write the quadratic equation in standard form. That is, using Properties of Equality, bring all
terms to one side of the equation so that the other side is equal to 0. Combine like terms, if
possible.
 •Factor relative to the integers.
 •Use the Zero Product Principle to solve. It states that if a product is equal to zero, then at least
one of the factors is equal to zero.

Problem 1:

Solve 15x^2 - 5x = 0 using the Factoring Method. Find any real and imaginary solutions.
The quadratic equation is already in standard form so that we can factor as follows:

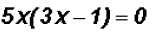
By the Zero Product Principle we can the say

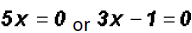
Therefore,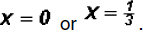

 Check:

Please note that if we check these solutions in the original equation, we find
the following:

Given 15x^2 - 5x = 0 and using x = 0, is 15(0)^2 - 5(0) equal to 0? Yes!
Therefore the solution is correct!

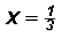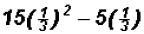Given 15x^2 - 5x = 0 and using , is equal to 0? Yes,
because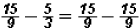 ! Therefore the solution is correct!

Problem 2:

Solve x^2 + 5x = -6 using the Factoring Method. Find any real and imaginary solutions.
Rewriting the equation in standard form yields x^2 + 5x + 6 = 0.
We notice that we have a trinomial, which we can factor as follows:

(x + 3)(x + 2) = 0

By the Zero Product Principle we can the say

x + 3 = 0 or x + 2 = 0

Therefore, x = -3 or x = -2.

Check:

Please note that if we check these solutions in the original equation, we find
the following:

Given x^2 + 5x = -6 and using x = -3, is (-3)^2 + 5(-3) equal to -6? Yes!
Therefore the solution is correct!

Given x^2 + 5x = -6 and using x = -2, is (-2)^2 + 5(-2) equal to -6? Yes!
Therefore the solution is correct!

Problem 3:

Solve x^2 - 4x + 4 = 0 using the Factoring Method. Find any real and imaginary
solutions.
We notice that we have a trinomial, which we can factor as follows:

(x - 2)(x - 2) = 0

By the Zero Product Principle we can the say

x - 2 = 0 or x - 2 = 0

Therefore, x = 2 in both cases. Sometimes the 2 is considered to be a double root.

B. Square Root Method - All quadratic equations can be solved by this method which uses the
Square Root Property. However, we might want to avoid this method for some quadratic equations
because it can get very cumbersome.

 •Isolate the squared term on one side of the equation. Be sure its coefficient is a positive 1 !!!!!!
 •Apply the Square Root Property.
 •If necessary, further isolate the variable.

The Square Root Property

If u is an algebraic expression containing a variable and d is a constant, then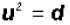
has exactly two solutions, namely
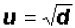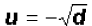and or simply