Math Homework Solutions
2.1.1. Show that there is an uncountable number of
Cauchy sequences of rational numbers equivalent to
any given Cauchy sequence of rational numbers.
Proof. Let α be any Cauchy sequence of rational numbers, and suppose
that
[ α ] { x l x is a Cauchy sequence and x is equivalent to α }
is countable. We would then have an enumeration of [ α ] , and thus
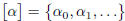
We define β to be the sequence such that for n ∈ N
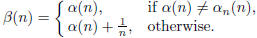
Clearly β is equivalent to α, since for each n, β(n) differs from α(n)
by at most 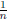 . However, we also
. However, we also
have 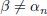 for all n since they differ in the nth
place. Thus β is not in the enumeration of [ α ], and
for all n since they differ in the nth
place. Thus β is not in the enumeration of [ α ], and
we have thus obtained a contradiction, so [ α ] is uncountable.
2.1.2. Show that every real number can be given by a Cauchy sequence of
rationals 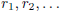 , where none
, where none
of the rational numbers 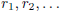 is an integer.
is an integer.
Proof. Let c be an arbitrary real number. If c is an integer, then the
sequence 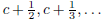 is a
is a
Cauchy sequence of rational numbers that converges to c, none of which are
integers.
Suppose that c is not an integer and let k be an integer such that k - 1 < c <
k. We construct a
sequence 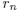 by arbitrarily choosing a rational
number from the interval
by arbitrarily choosing a rational
number from the interval 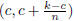 for each
for each
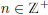 .
.
Clearly none of the 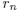 are integers, since c <
are integers, since c <
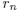 < k for all n, and
< k for all n, and
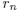 is equivalent to c, as desired.
is equivalent to c, as desired.
2.1.3. What kinds of real numbers are representable by Cauchy sequences
of integers.
Only integers are representable as Cauchy sequences of integers. To see this,
let 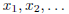 be any
be any
Cauchy sequence of integers. Then there exists
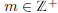 such that j, k ≥ m implies
such that j, k ≥ m implies
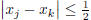 . If
. If
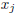 and
and 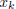 were
distinct integers, then
were
distinct integers, then 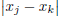 would be at least 1,
and thus we must have
would be at least 1,
and thus we must have 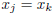 .
.
It follows that there exists 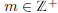 such that k ≥
m implies
such that k ≥
m implies 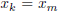 , and therefore x is equivalent
, and therefore x is equivalent
to the constant sequence 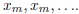
2.1.4. Suppose 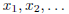 and
and
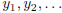 are two sequences of rational numbers.
Define the shuffled sequence
are two sequences of rational numbers.
Define the shuffled sequence
to be 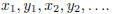 Prove that the shuffled sequence is a
Cauchy sequence if and only if
Prove that the shuffled sequence is a
Cauchy sequence if and only if 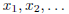
and 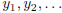 are equivalent Cauchy sequences.
are equivalent Cauchy sequences.
We will make use of the fact that a sequence is Cauchy if and only if it is
equivalent to some Cauchy
sequence to prove both implications.
Claim: If 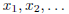 and
and
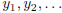 are equivalent Cauchy sequences, then the
shuffle sequence
are equivalent Cauchy sequences, then the
shuffle sequence
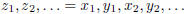 is a Cauchy sequence.
is a Cauchy sequence.
Proof. For any ![]() ,
there exists
,
there exists 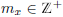 such that
such that
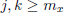 implies
implies 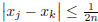 .
.
Similarly, since x is equivalent to y, there exists
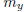 such that
such that 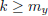 implies
implies 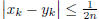 .
.
Let 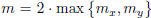 , and choose k ≥ m. If k is even,
then k = 2k' for some integer
, and choose k ≥ m. If k is even,
then k = 2k' for some integer
k'. It follows that 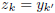 . It then follows that
. It then follows that
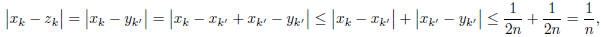
by the triangle inequality and since k and k' are greater
than both 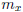 and
and
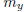 .
.
Otherwise, if k is odd, then k = 2k' − 1 for some integer
k'. Similarly, 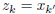 , and thus
, and thus
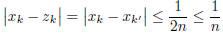
since both k and k' are greater than
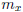 .
.
Thus, in either case 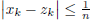 , so x and z are
equivalent, and z is Cauchy.
, so x and z are
equivalent, and z is Cauchy.
Claim: If 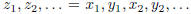 is a Cauchy sequence, then
is a Cauchy sequence, then
![]() and
and
![]() are
are
equivalent Cauchy sequences.
Proof. Since z is Cauchy, for every
![]() there exists m
such that j, k ≥ m implies
there exists m
such that j, k ≥ m implies
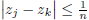 . In particular, if we let j = 2k − 1, then
. In particular, if we let j = 2k − 1, then
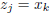 , and we have
, and we have
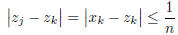
for all k ≥ m. Thus, z and x are equivalent, so x is
Cauchy. A similar proof shows that z and
y are equivalent, so y is Cauchy. Finally, since x is equivalent to z and z is
equivalent to y,
x is equivalent to y, by the transitivity of equivalence. Thus if z is Cauchy
then x and y are
both Cauchy and equivalent to each other.
2.1.8. Can a Cauchy sequence of positive rational numbers be equivalent
to a Cauchy sequence of negative
rational numbers?
Consider the sequence 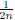 for
for
![]() and
and
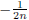 for
for
![]() . Clearly, for any
. Clearly, for any
![]() , we have
, we have
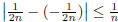 , and thus these two sequences are
equivalent.
, and thus these two sequences are
equivalent.
2.1.9. Show that if
![]() is a Cauchy sequence
of rational numbers there exists a positive integer N
is a Cauchy sequence
of rational numbers there exists a positive integer N
such that 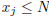 for all j.
for all j.
Proof. Let x be any Cauchy sequence, and suppose that for every integer N
there exists a j such
that 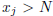 . Since x is Cauchy, there exists m such
that for all k ≥ m,
. Since x is Cauchy, there exists m such
that for all k ≥ m,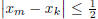 . Let N' be
. Let N' be
any integer greater than 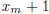 , and obtain j such
that
, and obtain j such
that 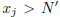 . If j m, then
. If j m, then
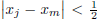 ,
,
which is impossible since 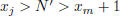 so
so
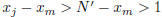 . Thus, j < m. Clearly, there
. Thus, j < m. Clearly, there
c an only be finitely many positive j that satisfy this inequality, and thus we
can take the maximum of
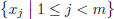 . The axiom of Archimedes guarantees that
there is an integer N that is larger than
. The axiom of Archimedes guarantees that
there is an integer N that is larger than
this maximum, and thus 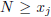 for all j. This is a
contradiction, so there must exist some integer
for all j. This is a
contradiction, so there must exist some integer
N such that 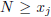 for all j.
for all j.




