Math Homework

Created and complied by Sherry Scarborough with thanks for additional problems from
Zach Barcevac, Lynnette Cardenas, Greg Klein, David Manuel, Jane Schielack, and Jenn
Whit eld.

1. How many positive divisors does 4840¹³ have?

2. What is the largest prime you would need to test to determine whether 161 is prime?

3. Is 161 prime? Show your work.

4. For a, b, c, ∈N, can 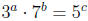. Explain why or why not.

5. Find the gcd and lcm of 360 and 525.

6. Give the formula that relates the gcd (t,w) and the lcm (t,w).

7. Find lcm(75,28,70).

8. Find gcd(8,12) and lcm(8,12).

9. "A prime number is any positive integer with exactly two distinct possitive divisors" is
the correct definition of a prime number. For each of the following incorrect definitions
of a prime number, give an integer that satisfies the false definition of prime number
and yet is not a true prime.

a. False definition: A prime number is any integer with exactly two distinct positive
divisors.

b. False definition: A prime number is any positive integer with two distinct positive
divisors.

c. False definition: A prime number is any positive integer with exactly two distinct
divisors.

d. Why is 2 not a prime number under the false definition given in part c?

10. Give an example of
a. two different prime numbers strictly between 25 and 75.

b. a composite number greater than 50.

c. a natural number that is neither prime nor composite.

11. Find the least whole number greater than 300 with exactly 3 positive divisors.

12. If 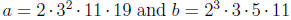, find gcd(a,b) and lcm(a,b). Leave your answers
written as a product of powers of primes.

13. Show the number 11638, the number 117, and the number 14875 are relatively prime.

14. Modular Arithmetic
a. 17 + 8 mod 5

b. 3 - 13 mod 7

c. 5/9 mod 24

d. 6 x 5 mod 5

e. 3/7 mod 8

15. Find three comsecutive natural numbers none of which is divisible by three. Explain
your answer.

16. a. For natural numbers a and b, if a|b, find gcd(a,b).

b. If a is a natural number, find lcm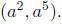

c. If lcm(a,b) = ab, find gcd(a,b).

d. For natural number n, find gcd(n,0).

e. If pa and q are distinct primes, find lcm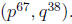

f. If b is a natural number, find gcd(b,b).

g. If lcm(a,b)=1, find a.

17. Find the remainder when 2⁷⁵ is divided by 8.

18. If d|a, does a/d divide a? Explain.

19. How many positive divisors does 936 have?

20. Use theorems 4-5 and 4-6 (pg. 233) to decide if 103 is prime or composite.

21. Classify and explain whether the following are true or false.
a. If gcd(a,b)=2, then a and b are both even.

b. If a and b are even, then gcd(a,b)=2.

22. List the first five composite numbers after zero.

23. Show two ways to find the prime factorization of 96.

24. Jennifer and Tom bought a 108-day special at a new fitness center. Jennifer will use
the fitness center every third day and Tom will use the center every fourth day. If they
both went the first day, how many days will neither use the fitness center?

25. Name two composite double-digit numbers that are relatively prime.

26. Use the Euclidean Algorithm and the appropriate theorem to find lcm(156,130).

27. "A school has a hall with 1,000 lockers, all of which are closed. A thousand students
start down the hall. The first student opens every locker. The second student closes all
lockers that are multiples of two. The third student changes (closes an open locker, or
opens a closed one) all multiples of three. The fourth student changes all multiples of
four. And so on. After all students have entered the school, how many lockers are closed
and which ones? (Brumbaugh, Ashe, Ashe, Rock, Teaching Secondary Mathematics,
Lawrence Erbaum Associates, New Jersey, 1997) Why?