Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Parabolas

To get started let’s look at a little bit of the history of the parabola. The first person to identify a parabola was
Menaechmus (375 – 325 BCE). He discovered the parabola during attempts to solve the three famous problems.
The parabola got its name from Apollonius of Perga (262 – 190 BCE). The focus and directrix of the parabola
were found by Pappus (290 – 350 CE). The parabola was first graphed on a Cartesian plane by Rene Descartes
(1596 – 1650 CE) in his book La géométrie around 1637. Also close to this time Galileo (1564 – 1642 CE)
recognized that objects follow a parabolic path due to gravity when given an initial velocity and direction.
James Gregory (1638 – 1675 CE) used the properties of the parabola to develop the combination telescope
(known as the Gregorian telescope), which used both mirrors and lenses thus making the length of the telescope
shorter while working more effectively than telescopes that used only lenses or only mirrors. Newton (1638 –
1675 CE) also studied the properties of the parabola in several contexts.

And now let’s discuss just what a parabola is. A parabola is a two-dimensional curve and by definition a
parabola is: the set of points in a plane satisfying the equations y = x² (or x = y²). This is also described as the set
of all points that are equidistant from a fixed line (called the directrix) and a fixed point (called the focus) not on
the directrix and symmetrical about an axis perpendicular to the directrix going through the focus.

Formulas often used are: y = ax²+ bx + c (general form) and y = a(x – h)² + k (vertex form) where the point
(h, k) is the vertex of the parabola.

Notice that when given the vertex form, the general form can be obtained by carrying out the multiplication of
the squared term and then combining all like terms. y = a(x – h)² + k

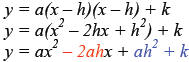
since a, h and k are all constants we can combine these terms in the following ways -2ah = b and ah² + k = c
and therefore we have the general form y = ax²+ bx + c

Using the standard form we can find the x-coordinate of the vertex with the expression:-b/2a
Also using the standard form we can find the equation of the axis of symmetry of the parabola with the
equation: x = -b/2a

We graph parabolas so that we can get a visualization of the quadratic equation that we are working with and so
that we can get approximations of the solutions of the quadratic equations. More importantly we graph
quadratic equations to model different situations that occur in the various aspects of our lives.

Home