Precalculus I Home Assignment

Print this document one-sided. If you are concerned about the environment, you may
use recycled paper. Solve all problems in space provided. If you need more space, you may
use the back of the page but be sure to indicate that in your solution. Each problem is
worth an equal amount of points. For every problem be sure to show all the work. Solutions
containing answers only will receive no or little credit. Make sure that your solutions are
written legibly.

Team-work is not forbidden and, actually, encouraged, however you are supposed to
submit solutions written by yourself.

You may use the textbook and notes as well as a scientific calculator to solve the problems.
This is all you will ever need!

If you have problems with understanding the assignment, please let your TA or me know
as soon as possible! Do not wait until the last minute!

Section 3.1

1. Suppose that f(x) = 4x - 1 and g(x) = -2x + 5.

a) Solve f(x) = 0
b) Solve f(x) > 0
c) Solve f(x) = g(x)
d) Solve f(x)≤g(x)
e) Graph y = f(x) and y = g(x) and label the point that represents the solution to
the equation f(x) = g(x)

2. Suppose that f(x) = 3x + 5 and g(x) = -2x + 15.

a) Solve f(x) = 0
b) Solve f(x) > 0
c) Solve f(x) = g(x)
d) Solve f(x)≤g(x)
e) Graph y = f(x) and y = g(x) and label the point that represents the solution to
the equation f(x) = g(x)

3. The cost C, in dollars of renting a moving truck for a day is given by the function
C(x) = 0.25x + 35, where x is the number of miles driven.

a) What is the cost if you drive x = 40 miles?
b) If the cost of renting the moving truck is $80, how many miles did you drive?
c) Suppose that you want the cost to be no more than $100. What is the maximum
number of miles that you can drive.

Section 3.3

4. Using the graph transformations graph f(x) = x^2 - 6x - 1

5. Using the graph transformations graph f(x) = 2x^2 - 4x + 1

6. Draw the graph of f(x) = 2x^2 - x + 2, determine if the graph opens up or down, find
the vertex, axis of symmetry, y-intercepts, x-intercepts, if any. Determine the domain
and the range of the function. Determine where the function is increasing/decreasing.

7. Draw the graph of f(x) = 4x^2 - 2x + 1, determine if the graph opens up or down, nd
the vertex, axis of symmetry, y-intercepts, x-intercepts, if any. Determine the domain
and the range of the function. Determine where the function is increasing/decreasing.

8. Determine without graphing whether the given quadratic function f(x) = -3x^2+12x+1
has a maximum value or a minimum value and then find the value.

9. Determine without graphing whether the given quadratic function f(x) = x^2 + 6x + 9
has a maximum value or a minimum value and then find the value.
 

10. The graph of the function f(x) ax^2 + bx + c has vertex at (0, 2) and passes through the
point (1, 8). Find a,b, and c.

11. Suppose that f(x) = x^2 + 4x - 21

a) What is the vertex of f?
b) What are the x-intercepts of the graph of f?
c) Solve f(x) = -21 for x. What points are on the graph of f?
d) Use the information obtained in the parts a) - c) to graph f(x) = x^2 + 4x - 21.

Section 3.4

12. The price p (in dollars) and the quantity x sold of a certain product obey the demand
equation

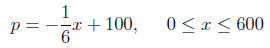
a) Express the revenue R as a function of x. (Recall: R = xp)
b) What is the revenue if 200 units are sold?
c) What quantity x maximizes revenue? What is the maximum revenue?
d) What price should the company charge to maximize revenue?

13. David has 400 yards of fencing and wishes to enclose a rectangular area.
a) Express the area A of the rectangular as a function of the width w of the rectangle.
b) For what value of w is the area largest?
c) What is the maximum area?

14. A farmer with 4000 meters of fencing wants to enclose a rectangular plot that borders
on a river. If the farmer does not fence the side along the river, what is the largest area
that can be enclosed?

15. A suspension bridge with weight uniformly distributed along its length has twin towers
that extend 75 meters above the road surface and are 400 meters apart. The cables are
parabolic in shape and are suspended from the tops of the towers. The cables touch the
road surface at the center of the bridge. Find the height of the cables at a point 100
meters from the center.