PYTHAGOREAN THEOREM AND DISTANCE FORMULA

APPLICATIONS

Solve the following problems. In solving these problems, keep in mind that
it is always helpful to draw pictures to guide your intuition and reasoning.

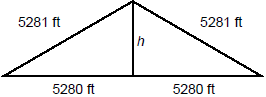
RAILROAD LINE PROBLEM: A high-speed railroad line was built through
the desert. In order to reduce derailments along a two-mile stretch, the
track was made using straight rails one mile long. The rails were laid in the
winter, and in the summer, due to the heat, each rail expanded one foot in
length. Ordinarily, the rails would push each other to the side, but in this
case they jutted upwards where the ends meet. How high above the
ground are the rails at the joints? (Historical note: when the RT Metro in
Sacramento, California was first running, the trains experienced a problem
similar to this situation.)

(This problem is adapted from College Preparatory Mathematics, Mathematics 1 (Algebra 1, Units 7-2) v. 3.2)

NOT DRAWN TO SCALE

EUCLID STREET PROBLEM: In order to go to school each day, Michelle
walks about 3 miles east from her home on Pythagoras Avenue, then walks
north along Euclid Street to the front of her school. She knows that the
shortest distance from her home to the front of the school is about 9 miles
(as the crow flies). How far does she walk along Euclid Street each school
day?

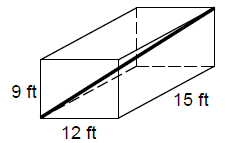
RECTANGULAR BOX PROBLEM: You have a huge rectangular box with
dimensions 9 ft. x 12 ft. x 15 ft. What is the length of the longest rod you
could fit in your box?

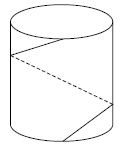
CYLINDRICAL CAN PROBLEM: The circumference of the base of a right
cylindrical can is 24 inches; the height is 7 inches. A shortest possible
spiral that winds once from the top to the bottom (see below) is painted on
the can, so that the bottom of the spiral is directly below the top of the
spiral. What is the length of the spiral?

JOURNAL

Four proofs of the Pythagorean theorem are sketched in the following
pages. Select one of the four proofs, study it, and figure out why it works.
Use the fourfold way to explain the proof. Be prepared to share your
findings with others.

FOUR PROOFS

First Proof

The Pythagorean theorem is well known to most high school geometry
students. What is not so well known is that there are numerous ways to
prove this famous theorem. On this page you have a diagram that
suggests a particular version of the proof. Your task is to complete the
proof along the lines suggested below. Be ready to present your proof to
the class.

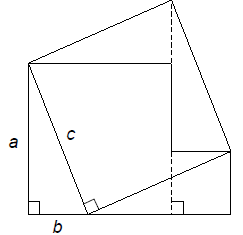
Proof sketch: Let A be the area of the entire figure. Let T be the area of the
right triangle with legs a and b and hypotenuse c. The figure contains four
congruent copies of the right triangle. (Why are they congruent?)
Decompose A in two different ways to see that

A = a² + b² + 2T,

A = c² + 2T.

Conclude that a² + b² = c².

Second Proof

James Abram Garfield (1831-1881) was elected the country’s twentieth
president in 1880. Earlier he had taught mathematics, and he discovered a
proof of the Pythagorean theorem in 1876, while he was a member of the
House of Representatives. Find Garfield’s proof of the Pythagorean
theorem using the diagram below and expressing the area of the trapezoid
in two different ways. Be ready to present your proof to the class.

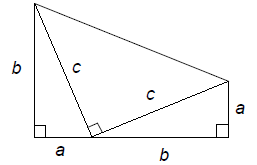
Proof sketch: Let A be the area of the entire figure, which is a trapezoid.
The area formula for the trapezoid is

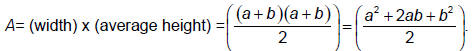
(Why is this formula true? You can find this formula by joining two copies
of the trapezoid together along the slanted edge to form a rectangle.)

Decompose the trapezoid into three triangles and express A as the sum of
the areas of three triangles,

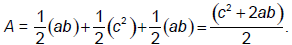
Equate these two expressions for A and conclude that

c² = a² + b².

Third Proof

On this page you have a diagram that suggests yet another version of the
proof. Your task is to prove the theorem using the decomposition of the
larger square suggested by the diagram below. Be ready to present your
proof to the class.

Proof sketch: Assume a ≤ b . Let A be the area of the largest square. Then

A = (a+b)².

Note that the side-length of the inside square is b-a. (Why?) Decompose A
into four rectangles and the inside square, to see that

A = 4ab + (b-a)² .

Equate these two expressions for A and conclude that

c² = a² + b².

Fourth Proof

On this page you have a diagram that suggests a version of the proof that
is closely related to the third proof. (How is it related?) Your task is to
prove the theorem using the decomposition of the square suggested by
the diagram. Be ready to present your proof to the class.

Proof sketch: Assume a ≤ b. Let A denote the area of the outside square.
Then

A = c².

The inside figure is a square (why?) with sides of length a - b (why?).
Decompose A into four triangles and the inside square, to see that

Equate these two expressions for A and conclude that

c² = a² + b².

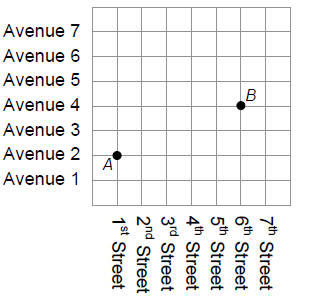
POINT A TO POINT B