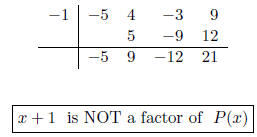SYNTHETIC DIVISION,THE REMAINDER THEOREM AND THE FACTOR THEOREM

Definitions:

• Dividend: The number or expression you are dividing into.
• Divisor: The number or expression you are dividing by.
• Synthetic division: is a quick method of dividing polynomials when the divisor is of the form x-c
where c is any constant (positive or negative).

Important Properties:

• Remainder Theorem: If a polynomial P(x) is divided by x - c, then the remainder is P(c). This
gives us another way to evaluate a polynomial at c.
• Factor Theorem: c is a zero of P(x) if and only if x - c is a factor of P(x).

Steps for synthetic division to divide P(x) by x - c: Synthetic division will consist of three rows.

1. Write the c and the coefficients of the dividend in descending order in the first row. If any x terms
are missing, place a zero in its place.
2. Bring the leading coefficient in the top row down to the bottom (third) row.
3. Next, multiply the first number in the bottom row by c and place this product in the second row
under the next coefficient and add these two terms together.
4. Continue this process until you reach the last column.
5. The numbers in the bottom row are the coefficients of the quotient and the remainder. The quotient
will have one degree less than the dividend.

Example: Divide P(x) = 2x⁴ - 8x³ + 5x² + 4 by x - 3.

First, note that the x term is missing so we must record a 0 in its place.

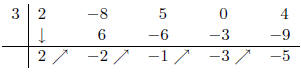
Therefore, the quotient is 2x³ - 2x² - x - 3 and the remainder is -5.

Common Mistakes to Avoid:

• Do NOT forget to record a zero for any missing terms. For example, suppose the dividend is
f(x) = 3xA⁴ - 5x² - 2. Since both the x³ and x terms are missing we would record the coefficients as
3 0 - 5 0 - 2.
• Remember to add the terms inside the synthetic division process.
• If the divisor is x + c, then the number outside the synthetic division is -c. For example, if the
divisor is x + 5 then we record a -5 on the outside of the synthetic division.

PROBLEMS

1. Use synthetic division to find each quotient.

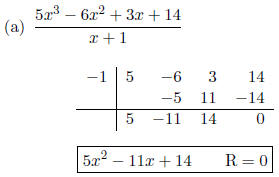
Note that the x² term is missing. Do
not forget to place a zero in its place.

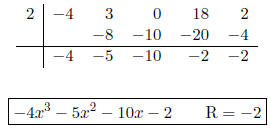
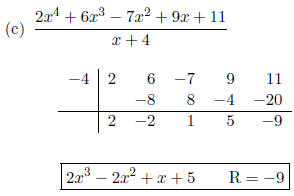
Note that the x term is missing. Do not
forget to place a zero in its place.

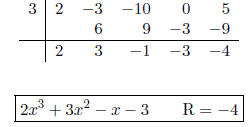
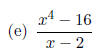
Note that the x³, x² and the x terms
are all missing. Therefore, zeros must
be recorded in their places.

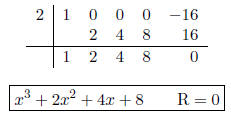
2. Use the remainder theorem to find P(c).
(a) P(x) = 2x³ - 5x² + x + 4; c = 1

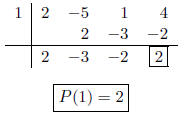
(b) P(x) = 4x⁴ +5x² -9x+7; c =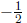

Note that the x^3 term is missing. Do
not forget to record a zero in its place.

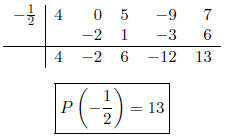
3. Use the factor theorem to determine whether
x - c is a factor of P(x).
(a) P(x) = 2x³ -7x² -10x+24; c = 4

Remember that x-4 is a factor of P(x)
if and only if 4 is a zero of P(x). There-
fore, x-4 is a factor if we end up with
a zero remainder.

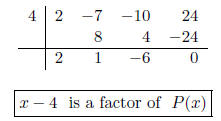
(b) P(x) = -5x³+4x²-3x+9; c = -1

Remember that x+1 is a factor of P(x)
if and only if -1 is a zero of P(x).
Therefore, x + 1 is a factor if we end
up with a zero remainder.