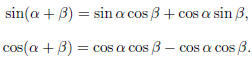What you need to know to take Calculus 221

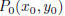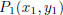§9. By the Pythagorean theorem the distance from to is

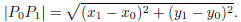
The distance from a point P(x, y) to the point 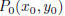is exactly a when




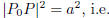
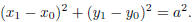
This is the equation for the circle centered at 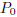with radius a. (See Appendix C
page A17.) For example, the equation of the circle of radius 5 centered at
is

(x − 2)² + (y − 3)² = 5², or x² + y² − 4x − 6y − 12 = 0.

The latter equation has the form of a general 2nd degree equation

Ax² + Bxy + Cy² + Dx + Ey + F = 0

(with A = C = 1, B = 0, D = −4, E = −6, F = −12); ellipses (including
circles), parabolas, and hyperbolas all have equations of this form.

4 Precalculus

This material will be reviewed as we need it, but you should have
seen it before.

§10. A function is a rule which produces an output f(x) from an input x. The
set of inputs x for which the function is defined is called the domain and f(x)
(read “f of x”) is the value of f at x. The set of all possible outputs f(x) as x
runs over the domain is called the range of the function. For example, for the
function f(x) = 1/x² the domain is the set of all nonzero real numbers x (the
value f(0) is not defined because we don’t divide by zero) and the range is the
set of all positive real numbers (the square of any nonzero number is positive).
For the function y = sinθ the domain is the set of all real numbers θ and the
range is the set of all real numbers y such that −1≤ y ≤1.

§11. The graph of a function

y = f(x)

is the set of all points P(x, y) whose coordinates (x, y) satisfy the equation y =
f(x). More generally, an equation of form

F(x, y) = 0

determines a set (graph) in the (x, y)-plane consisting of all points P(x, y) whose
coordinates (x, y) satisfy the equation. The graph of a function y = f(x) is a
special case: take F(x, y) = y−f(x). To decide if a set is the graph of a function
we apply the

Vertical Line Test. A set in the (x, y)-plane is the graph of a
function if and only if every vertical line x = constant intersects
the graph in at most one point. [If the number k is in the domain,
the vertical line x = k intersects the graph y = f(x) in the point
P(k, f(k)).]

§12. For example, the graph of the equation x² + y² = 1 is a circle; it is not
the graph of a function since the vertical line x = 0 (the y-axis) intersects the
graph in two points 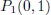and 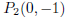. This graph is however the union of
two different graphs each of which is the graph of a function:



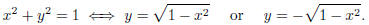
§13. In calculus, we learn to reason about a function even when we cannot find
an explicit formula for it. For example, in theory the equation x = y⁵+y (which
has the form x = g(y)) can be rewritten in the form y = f(x) but there is no
formula for f(x) involving the mathematical operations studied in high school.

§14. When two functions are related by the condition

y = f(x) x = g(y)

(for all appropriate x and y) we say that the functions are inverse to one
another and write g = f ^-1. Then the range of f is the domain of g and vice
versa. Often a function f has an inverse function g only after we modify f
by artificially restricting its domain. The following table lists some common
functions (suitably restricted) and their inverses.

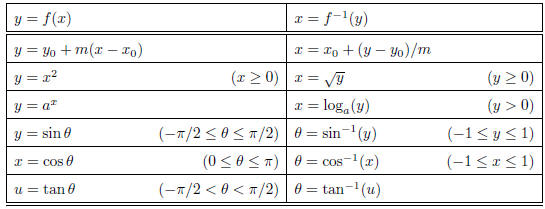
(The notations arcsin y = sin^-1 y, arccos x = cos^-1 x, and arctan u = tan^-1 u
are also commonly used for the inverse trigonometric functions. The exponential
function y = a^x is only defined for a positive.) To decide if a function has an
inverse we apply the

Horizontal Line Test. A function has an inverse if and only if
every horizontal line y = constant intersects the graph in at most
one point. [The horizontal line y = k intersects the graph y = f(x)
in the point P(f ^-1(k), k).]

5 Trigonometry

There is a review of trigonometry in section 2-9 of the text but you
should already be familiar with this material. You should also have
seen the inverse trigonometric functions before. These are reviewed
in section 6-2.

§15. In calculus we always measure angles in radians rather than degrees. The
radian measure of an angle is the arclength of a circle of radius one (centered
at the vertex of the angle) cut out by the angle. Since the total length of the
circumference of a circle is 2π we get

2π radians = 360°.

(Since 2π = 6.283 . . . is about 6, this means that one radian is a little less than
60 degrees.)

Let P(x, y) be a point of the (x, y) plane, O(0, 0) denote the origin, r = |OP|,
and θ denote the angle between the positive x-axis and the ray OP. Then

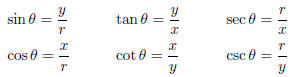
Since r is positive (· always means the positive square root) these formulas
make it easy to remember the symmetries



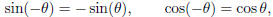
(which say that the sine is an odd function and the cosine is an even function)
and the sign reversals



All the trigonometric functions have period 2π :



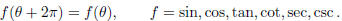
Because of the above sign reversal formulas for the sine and cosine and the
equations

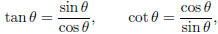
the tangent and cotangent have period π:



The cofunction of an angle is the function of its complement:
.
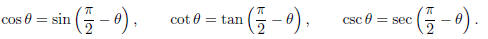The trigonometric addition formulas are