Answers to Examples Used in Fundamental Theorem of Algebra Notes
Write each polynomial in irreducible factored form over
the set of real numbers and as the product of
linear factors over the set of complex numbers. Identify which zeros correspond
to x-intercepts and
which do not correspond to x-intercepts.
1. f(x) = x2 – 1
= (x–1)(x+1) is both Irreducible Factored Form and Complex Linear Factored Form
x = 1 and x = –1 are zeros and x intercepts
2. f(x) = x2 + 1 Irreducible Factored Form
= (x– i)(x+ i) Complex Linear Factored Form
x = i and x = – i are zeros but not intercepts. f(x) has does not have any x
intercepts
3. f(x) = x2 – 5
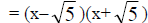 is both Irreducible Factored Form and Complex Linear Factored Form
is both Irreducible Factored Form and Complex Linear Factored Form
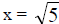 and
and 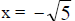 are zeros and x intercepts
are zeros and x intercepts
4. f(x) = x2 + 5 Irreducible Factored Form
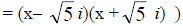 Complex Linear Factored Form
Complex Linear Factored Form
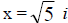 and
and 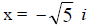 are zeros but not intercepts; f(x) has does not have any x
intercepts
are zeros but not intercepts; f(x) has does not have any x
intercepts
5. f(x) = x6 – 24x4 – 25x2
= x2(x4 – 24x2– 25)
= x2(x2 –25) (x2 +1)
= x2(x –5) (x +5) (x2 +1) Irreducible Factored Form
= x2(x –5) (x +5) (x– i)(x+ i) Complex Linear Factored Form
x = 0, 5, –5, i, – i are zeros; x = 0, 5, –5, are x-intercepts
The graph crosses the x-axis at x = 5 and x = –5
x = 0 is a zero of even multiplicity 2, so the graph touches but does not cross
the x-axis at x = 0
x2 is a repeated linear factor (x–0)2
6. f(x) = x3 + 4x2 – 2x – 8
= x2 (x+4) – 2(x+4)
= (x2 – 2) (x+4)
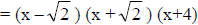 both Irreducible Factored Form
both Irreducible Factored Form
 and Complex Linear Factored Form
and Complex Linear Factored Form
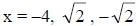 , are zeros and x intercepts
, are zeros and x intercepts
7. f(x) = x3 – 3x2 +8x – 24
= x2 (x – 3) +8 (x – 3)
= (x2 + 8) (x – 3) Irreducible Factored Form
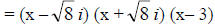 Complex Linear Factored Form
Complex Linear Factored Form
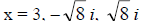 are zeros ; x = 3 is the only x intercept
are zeros ; x = 3 is the only x intercept
8. f(x) = x2 + 2x + 3 Irreducible Factored Form
Irreducible Quadratic x2 + 2x + 3 can’t be factored over set of real numbers:
use quadratic formula to
find complex zeros and use the complex zeros to create the factors.
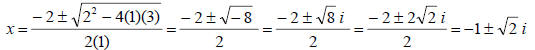
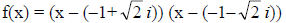 Complex Linear Factored
Form
Complex Linear Factored
Form
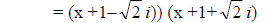
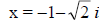 and
and 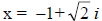 are zeros but not intercepts; f(x) has does not have any
x intercepts
are zeros but not intercepts; f(x) has does not have any
x intercepts
9. f(x) = x3 + 64 sum of two cubes
= (x+4)(x2 – 4x + 16) Irreducible Factored Form
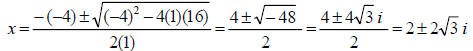
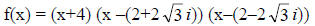 Complex Linear
Factored Form
Complex Linear
Factored Form
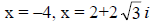 and
and 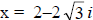 are zeros ; x = –4 is the only x intercept
are zeros ; x = –4 is the only x intercept
10. f(x) = x3 – 64 difference of two cubes
= (x–4)(x2 + 4x + 16) Irreducible Factored Form
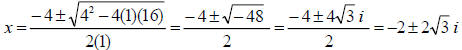
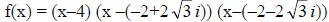 Complex Linear
Factored Form
Complex Linear
Factored Form
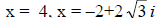 and
and 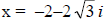 are zeros: x = 4 is the only x intercept
are zeros: x = 4 is the only x intercept
11. f(x) = x9 – 4x8 + 5x7
= x7 (x2 – 4x + 5) Irreducible Factored Form
x7 is a repeated linear factor (x–0)7
(x2 – 4x + 5) does not factor over the set of real numbers – it is irreducible.
Use quadratic formula to find complex zeros and use them to create the factors.
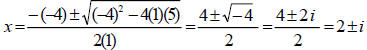
f(x) = x7 (x –(2+i)) (x–(2–i)) Complex Linear Factored
Form
x = 0, x = 2+i and x = 2–i are zeros
x7 is a repeated linear factor (x–0)7
x = 0 is the only x intercept, of multiplicity 7;
The graph crosses the x axis once, at (0,0) and it flattens out as it crosses
because x = 0 is a zero of odd multiplicity greater than 1
The answer to number 12 was printed on the back side of
your handout for Fundamental Theorem of
Algebra, so is not posted here.




