ELEMENTARY NUMBER THEORY PAPER TOPICS

The paper should be 3-5 pages in length, if your paper is slightly shorter or substantially
longer, you will not be penalized. It should have an introduction and a conclusion, and
clearly-written proofs and examples. Your target audience for the paper should be your
peers, imagine coming back to this paper after two years, will you still be able to follow it
from start to finish?

You must choose a topic by Friday, March 20. You must both send me an e-mail
and talk to me (before or after class, in office hours, or by appointment) so that I can suggest
further reading and directions. A good place to start will be consulting what the text has
to say, but I will push you to look beyond this resource.

It is strongly recommended that you turn in a rough draft of your paper to me sometime
in April|even one only partially finished-|so that I can give you feedback. The quality of
my comments will be proportional to the amount of time that you give me to look at it.
The paper is due Friday, April 24, 2009. Please note that the last day of class is
Wednesday, April 29, and that there will be no final examination.

The paper may be hand-written, but if so you must use an impeccable script. (If you
would like to use 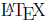, come talk to me and I'll help you get started.)

Here are some possible topics.

• Transcendental numbers: What can you say about the proof that e (or π ) is tran-
scendental?
• Axioms for integers: Compare the axiomatic definitions of the integers (called Peano
arithmetic), and prove from this set of axioms that it has the least element property.
• History: Choose your favorite theorem(s) and describe the historical background of
its discovery, including a biography of its originator.
• Fermat's last theorem: Show that xⁿ + yⁿ = zⁿ has no solutions x, y, z ∈ Z with
xyz ≠ 0 for n = 3 or n = 4 (Section 13.2).
• Euclidean algorithm for Gaussian integers: Define the Gaussian integers Z[i] and
show that it too has a Euclidean algorithm (Sections 14.1{14.2).
• Rings without unique factorization: Show that 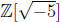does not have unique factor-
ization (Exercises 3.5.19{3.5.24).
• Lagrange's four squares theorem: Show that every positive integer n is the sum of 4
squares, n = x² + y² + z² + w² (Section 13.3).
• Bertrand's conjecture: Show that if n is a positive integer, then there exists a prime
p such that n < p < 2n (Exercises 3.2.23{24).
• Twin primes: What can you say about the (conjectured) distribution of twin primes?
Periodic decimals: Given a rational number a/b with gcd(a, b) = 1, prove that it has
a repeating decimal. What can you say about its period length?
• Pell's equation and continued fractions: Show that x² - Dy² = 1 has an integer so-
lution x, y ∈ Z whenever D ∈ Z>0 is squarefree, and relate this solution to continued
fractions.
p-adic numbers: De ne the ring 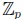of p-adic integers as the completion of Z under
the absolute value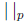. What can you say about the topological properties of this
space?
• Odd perfect numbers: What is currently known about the nonexistence of odd perfect
numbers?
• Tournament scheduling: How can congruences be used to schedule round-robin tour-
naments (Section 5.3)?
• Mersenne primes: Investigate what is known about Mersenne primes. In particular:
how does one test whether a given Mersenne number is prime? what is the complexity
of this method? which are the known Mersenne primes?
• Farey fractions: What is the relationship between Farey sequences and rational ap-
proximations to irrational numbers?
• Distribution of primes: Give some elementary estimates for π (x).
• Riemann hypothesis: What is the Riemann hypothesis, and how does it relate to the
distribution of primes?
• ABC conjecture: What is the ABC conjecture? What is the best known ABC triple?
• Quadratic residues, coin- ipping by phone Is there a way for two people to remotely
ip a coin fairly? Can you convince someone you have some information without
revealing it?
• Cryptography: How is number theory useful in cryptography?